Task:Define voting procedure for Community Council elections
| This is an ongoing task, planned to be completed during the current maemo.org development sprint. Any help is appreciated! Please see the talk page for discussion. |
Due to the noise generated by the voting procedure from the first election, the procedure needs to be reevaluated and a better system needs to be put in place for the next election.
Contents |
Proposal: RRV
Variables
- l: number of voters
- m: number of candidates
- n: number of seats
- i: index of voters (
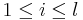 )
)
- j: index of candidates (
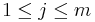 )
)
- k: index of seats (and rounds) (
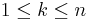 )
)
Parameters
A range for votes is selected by two limits, amax and amin. Reasonable choices include:
- amin = 0, amax = 1 (unbalanced, normalized)
- amin = − 1, amax = 1 (balanced)
- amin = 0, amax = 100 (unbalanced percentage; potentially useful if ratings were to be quantized)
The effects of the voting system are generally independent of the limits selected, but a balanced range may be preferred by some voters to permit unknown candidates to be rated 0 with known, disliked candidates rated negative. Obviously this effect may be accomplished in an unbalanced range by rating unknown candidates 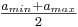 . Some calculations are simplified by using the unbalanced, normalized range, which makes it preferable from a numerical perspective.
. Some calculations are simplified by using the unbalanced, normalized range, which makes it preferable from a numerical perspective.
A ballot from voter i consists of m ratings aij for the m candidates, such that 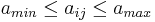 .
.
Procedure
After all ballots are collected, n rounds are held to choose the winners wk, with one winner chosen per round. In the first round, the weighted ratings for each voter are initialized as bij1 = aij. The weighted scores in each round are summed:
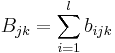
The highest-scoring candidate not yet elected wins; this is not simple to express formally:
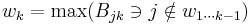
The weighted scores for each succeeding round are calculated by de-emphasizing ballots according to the portion in which they've already won:
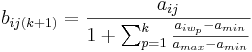
In the case of an unbalanced range (amin = 0), 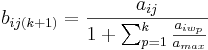 , and in the normalized case (amax = 1),
, and in the normalized case (amax = 1), 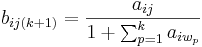 .
.
